112 12. Worksheet on the

Algebra & Coordinate Geometry of Circles

There are two objectives of this worksheet.

1. Know the forms and be able to recognize the equation of a circle.

2. Given enough information about a circle, be able to either

a. Graph the circle or

b. Write the equation of the circle

All of these objectives are obtained from two things, the distance formula and the definition of a circle.

The distance formula comes from

Pythagoras' theorem - The sum of the squares of the sides of a right triangle equals the square of the hypotenuse of said triangle.

From coordinate geometry, this becomes (see picture below)

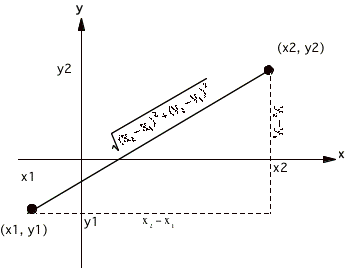
So the distance between these two points becomes

The Definition of a Circle is - the set of all points in the xy plane a fixed distance r, (called the radius) from a fixed point(h,k) (called the center). Using the above definition of distance, then the point in the plane (x,y) is on the circle whose center is (h,k) and radius is r, if and only if

= r². Or, since both sides are always going to be positive, we could square both sides and have a less formidable looking representation

of a circle, = r²
So any equation in the above form represents a circle with radius r and center (h,k)

Examples: Equation to Graph

has center = (3,4) and radius r = 5 ;

notice the Domain = [3 -5, 3 +5]= [-2, 8) , and the range = [4 - 5, 4 + 5] = [-1, 9).

has center = (-3,1) and radius r = 4

D = ? R = ?

has center = (0,-4) and radius r = 3

D = ? R = ?

has center = (3,-5) and radius r = √3

D = ? R = ?

does not represent a circle.

There are no ordered pairs of real numbers satisfying the equation. Any time you have an equation of the form (x - h)² + (y - k) = C and the C is negative, the equation has no real solution.

Examples: Graph to equation

The circle with center (1, -4) and radius r = 4 has equation

The circle with center (-2, -5) and radius r = 1 has equation

The circle with center (0,0) and radius 8 has equation x² + y² = 64

The Big Picture of circles.

If any of the above equations were multiplied out and simplified, the result would look like

Ax² + Ay² + Cx + Dy = E, where C, D, and E are real constants. This is the General Form of a circle. So anytime you see an equation that can be expressed in this form, you must recognize it as the equation of a circle. You should also be able to write it in the standard form

(x-h)² + (y-k)² = r²

from which you can find the center, radius, and graph, along with the domain and range. You will accomplish the conversion by
completing the square on both the x terms and the y terms.

Recall (x + a)² = x² + 2ax + a²

so for a quadratic expression x² + bx + c to be a binomial square, the constant term c must be c = (b/2)²

To put it the other way around,

to make x² + kx a binomial square,

we'd have to add the constant term (k/2)² to it.

Examples of General to standard.

Example 1: x² + y² - 6x + 12 y + 20 = 0

First, rewrite the equation in the following form.

x² - 6x + _________ + y² + 12y + __________ = - 20 + ________ + ________

Next decide what goes in the blanks on the left by completing the square in both x and y expressions, and don't forget to include these terms on the right side as well to keep the equation valid.

Here's how to complete the square:

(-6/2)² = (-3)² = 9 and (12/2)² = 6² = 36, so the blanks above become

x² - 6x + 9 + y² + 12y +36 = - 20 + 9 + 36 , which, in standard form is written

(x - 3)² + (y + 6)² = 25

Whereupon we can now easily extract the center = (3, -6) and radius 5, which we could then graph.

D = ? R = ?

Example 2: x² + y² +8x -6y + 9 = 0

Solution:

x² + 8x +16 + y² - 6y + 9 = -9 + 16 + 9

(x + 4)² + (y - 3)² = 1, so

center = (-4, 3) and radius = 1

Example 3: x² + y² +8x -6y + 8 = 0

x² + 8x +16 + y² - 6y + 9 = -8 + 16 + 9

(x + 4)² + (y - 3)² = 17, so

center = (-4, 3) and radius = √17

Example 4: x² + y² +8x -6y +25 = 0

x² + 8x +16 + y² - 6y + 9 = -25 + 16 + 9

(x + 4)² + (y - 3)² = 0, so

center = (-4, 3) and radius = 0, this circle is a single point, the center!

Example 5: x² + y² +8x -6y + 29 = 0

x² + 8x +16 + y² - 6y + 9 = -29 + 16 + 9

(x + 4)² + (y - 3)² = -4, so this circle doesn't exist, since √-4 is not a real number.

Problems:

1. x² + y² - 2x -10y = 55 sol: C = (1,5) and r = 9

2. x² + y² + 4x + 10 y + 13 = 0 sol: C = (-2, -5), r = 4

3. x² + y² - 12x + 10 y + 13 = 0 sol: C = (6, -5), r = 4 √3