Math 112 17. Worksheet
on VA's & HA's
Graphing Rational Functions Using
Vertical & Horizontal Asymptotes
There are basically two steps to this
objective.
1. Finding HA's & VA's
2. Deciding where the graph goes .
Step 1, finding horizontal and vertical
asymptotes, requires some understanding of a new number, infinity, which is
denoted by the symbol °. Infinity
is an unimaginably large number.
You can think of it as the number at the end of the number line. When the value of a fraction becomes
large without bound, we say it "goes to infinity".
However, infinity is NOT a real number, so when a rational function "goes to infinity
" at a particular value of x, we must say that it is not defined at that
value of x, and that value of x is not in the domain of
the function.
For rational functions, the value of the
function goes to infinity for x values at which the denominator is zero and the
numerator is not zero. If you were
to draw a graph of the function near these x values, the graph would begin to
look like a vertical line as x nears one of these values.
Illustration:
look at the function f(x) = 
The
denominator "has a zero" (which means the denominator equals zero) at
x = 3. As x nears the value 3,
from either side, the function values begin to get closer and closer to points on the line x = 3. So we say the line
x = 3 is a vertical asymptote for this function.
In brief then, to find vertical
asymptotes of a rational function, simply look for zeros of it's denominator.
Example 1: 
has a VA at x = 4, and 4 is not in the domain of the
function.
Example 2: 
has two VA's, x = 2 and x = -2, and the domain of f is all
reals except these two numbers.
Example 3: 
has no VA's since x2 + 4 = 0 has no real solution.
Problems: Find the VA's for
1.
, the answer is x = 4
2.
, the answer is x = 4 and x = -4
3.
. this function has no VA's
4.
, the answer is x = 5/3 and x = -1
5.
, the answer is x =0, x = 3, x = -5, x = -8
Finding the horizontal asymptotes of a
rational function.
Finding HA's requires asking the question,
does the function value approach a real number as x goes to infinity?
Finding the answer is easy if you remember
a very important fact about polymomial functions, which is the dominance of the
term of highest degree as x goes to infinity.
Illustration:
What this means is that as x gets large,
f(x) = 3x4 - x3 +
912 x2 + 4x - 87000 begins to look like
g(x) = 3x4 , simply because as
x gets large, the value of 3x4 increases so much faster than the
values of the other terms that their effect on the value of f (x) becomes
insignificant.
So to find the horizontal asymptotes of a
rational function, we simply throw away all but the leading term in numerator
and denominator, reduce the resulting fraction, and evaluate it at x = °.
Example 1:
becomes 
, which approaches zero as x goes to
infinity, so the HA is y = 0
Example 2:
becomes 
= 3 regardless of the value of x, so the HA is y = 3
Example 3: 
becomes 
= 3x , which approaches ° as x goes to infinity, so this
function has no HA.
Problems: Find the HA for
1.
, the answer is h = 2
2.
, the answer is s = 2/3
3.
, the answer is p = 0
4.
, the answer is no HA
5.
, the answer is r = 0
Step 2 : Finding
where the graph goes, is
the really big step. But, since
rational functions are smooth continuous curves except where they are
undefined, it is not as difficult as one would imagine. Usually, simply remembering this fact
and using the x and y intercepts one
can draw the curve without finding any other points. It is also helpful to remember
that the curve never intersects the VA's, but can intersect the HA's as many times as is necessary. It is also highly recommended that you
follow a set routine everytime you graph a rational function, and here is that
routine.
Steps to graphing rational functions.
1.
Find x intercepts (by replacing f(x) with a zero and solving for x.)
2.
Find the function or y intercept (by replacing the x by zero and solving
for f(x) ).
3.
Find VA's (by finding zeros
of the denominator)
4.
Find the HA (by eliminating all but the leading term in numerator and
denominator and solving for f(x)).
5.
Plot the intercepts, and draw in the VA's and the HA as dotted lines.
6.
The x intercepts and VA's divide the x axis into regions. Beginning on the left end of the x
axis, carefully draw the curve over each region, obtaining other sample points
as necessary.
Example 1:
¥ solving 
for x gives x intercept x = 0
¥ replacing
x by zero in the function gives f intercept f(0) = 0
¥
Solving x-3=0 gives VA x = 3
¥ Reducing
the function f(x) = 2x / x = 2 gives the HA f = 2
¥ The
x intercept and VA divides the x axis into three regions, (-°, 0), (0, 3), and
(3, °). Here are the graphs
over each region:
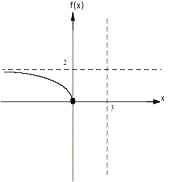
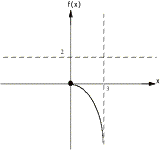
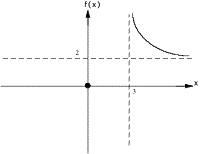
putting them all together we have
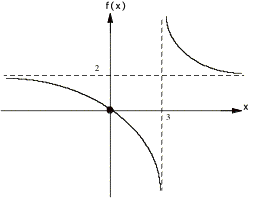
Example 2:
¥ Solving 
for x yields x = 3 as the only x intercept.
¥ Finding
h(0) by replacing x by zero yields the h intercept as h = 3/2
¥ Solving
x2 + x - 2 = 0 gives VA's x = -2 and x = 1
¥ Reducing
the function h(x) = x / x2 = 1/x and evaluating as x goes to °, gives h = 0 as the HA
¥ The
x intercept and VA's divide the x axis into 4 regions: (-°, -2), (-2, 1), (1,3), and
(3,°). Here are graphs over each
region.
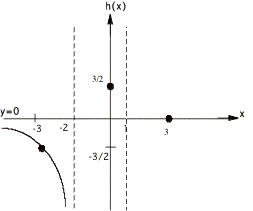
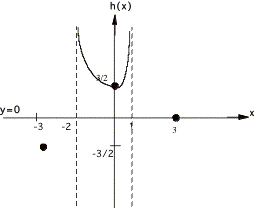
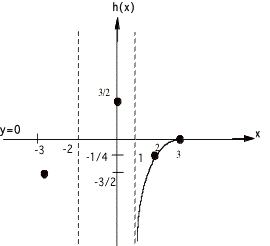
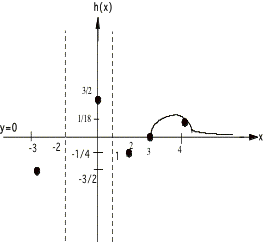
putting it all together we have:
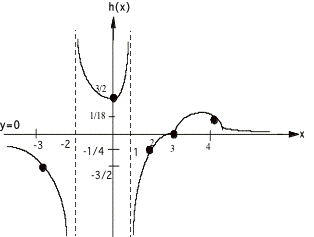
Notice that I had to find test points in
the first, third and fourth regions, and note too that my graph is not to
scale, I just made it so that the solution is clear.
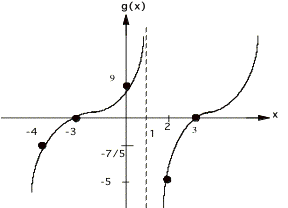
Example 3: 
¥ Solving
0 = x2 - 9 yields x = 3 and x = -3 as x intercepts. (What happened to the denominator, why
did I apparently throw it away?)
¥ Finding
g(0) by replacing x by zero gives a g intercept of 9
¥ Solving
x - 1 = 0 for x gives VA x = 1
¥ Reducing
g(x) = x2 / x =x and evaluating as x goes to ° gives g = °, so there
is no HA.
¥ The
x intercepts and VA's divide the x axis into four regions , (-°, -3), (-3, 1),
(1,3), and (3, °). Here are the
graphs over each region.
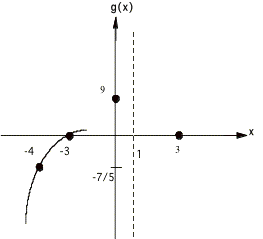
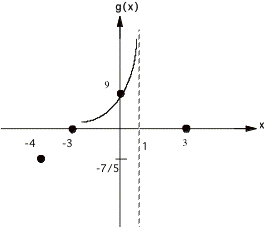
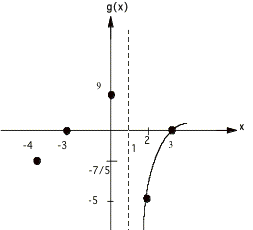
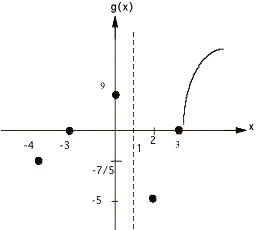
putting them all together looks like this
Problems: Find x & y
intercepts, VA's & HA, and sketch
1.
2.
3.
