Math 110 Final Exam Review Version 1 20 points each Dec. 12, 2002

1. Find the slope of the line between (-2, 1) and ( 3,4)

2. An office building worth one million dollars when completed in 2000 is being depreciated linearly over 50 years. (Assume scrap value of $0). What will be the book value of the building in 2010?

3. Write the system of equations corresponding to the given augmented matrix.

4. Solve the system of equations.

x - 2y = 2

7x -14 y = 14

3x - 6y = 6

5. A nutritionist at the Medical Center has been asked to prepare a special diet for certain patients. She has decided that the meals should contain a minimum of 400 mg of calcium, 10 mg of iron, and 40 mg of vitamin C. She has further decided that the meals are to be prepared from foods A and B. Each ounce of food A contains 30 mg of calcium, 1 mg of iron, 2 mg of vitamin C, and 2 mg of cholesterol. Each ounce of food B contains 25 mg of calcium, 0.5 mg of iron, 5 mg of vitamin C, and 5 mg of cholesterol. Find how many ounces of each type of food should be used in a meal so that the cholesterol content is minimized and the minimum requirements of calcium, iron, and vitamin C are met.

6. Find the accumulated amount A if the principal P is invested at the interest rate r per year for t years.

P = $150,000 , r = 12 %, t = 3 years, compounded daily.

7. 1. Find the amount (future value) of the ordinary annuity:

$1800 per quarter for 6 years at 8% per year compounded quarterly.

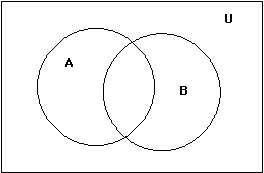
8. Shade the region A^c _ B

9. How many three-letter code words can be constructed from the first 10 letters in the Greek alphabet if no repetitions are allowed?

10. P(6, 4) =

11. In how many ways can a subcommittee of four be chosen from a Senate committee of five Democrats and four Republicans if:

a. all members are eligible?

b. the subcommittee must consist of two Democrats and two Republicans?