13. Page 223

1,3,5,8,9,11,12,21,22,23,30,33,37,38,40,42

and as many of the "C" problems as you please for 5 Points Bonus each!

1. Find the two numbers x and y whose sum is 48 and whose product is a maximum.

3. A farmer wants to fence in 60,000 m² of land in a rectangular plot along a straight highway. The fence along the highway costs $10 per meter, while the fence for the other three sides costs $5 per meter. How much of each type of fence will have to be bought in order to keep expenses to a minimum? What is the minimum expense?

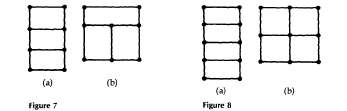
5. A farmer wants to fence in 180,000 sq ft of land in a rectangular plot and then divide it into three equal plots with a pair of fences both parallel to the same pair of sides (see Figure 7a). What is the least amount of fence needed to accomplish this?

Figures 7,8

8. A square piece of cardboard with each side 12 cm long has a square cut out at each corner. The sides are then turned up to form an open box. Find the side of the cut-out square that will produce a box of maximum volume.

9. A rectangular box, open at the top, with a square base, is to have a volume of 4000 cm³. What must be its dimensions if the box is to require the least possible material?

11. Find the dimensions of the rectangle of greatest area with its base on the x axis and its other two corners above the x axis and on

12. Find the dimensions of the trapezoid of greatest area inscribed in and having its longer base on the x axis.

21. A tin can is to be made with a capacity (that's volume) of 2cm³. What dimensions will require the smallest amount of tin? Note: The volume of a right circular cylinder in V=¹r² h, where h is the height and r is it's radius. The area of a circle is A = ¹r².

22. Find the point on y² = 4x closest to (-8,0).

23. Find the point in the first quadrant on xy=3 closest to (-8,0).

The C problems are problems 30 - 42 below!!

30. The strength of a wooden beam of a given length is proportional to its width and the square of its height. Find the dimensions of the strongest beam that can be cut from a circular log of diameter 1.5m.

33. A man is in a boat 4 miles off a straight coast. He wants to reach a point 10 miles down the coast in the least possible time. If he can row 4 miles per hour and run 5 miles per hour, where should he land the boat?

37. The current I in a voltaic cell is

where E is the electromotive force and R and r are the external and internal resistance, respectively. E and r are internal characteristics of the cell; they cannot be changed. The power developed is P = RI². Show that P is a maximum when R=r.

38. The efficiency of a screw is given by the formula

where is the coefficient of friction and h is the tangent of the pitch angle of the screw. Find the value of h for which the efficiency is a maximum.

40. The cost of fuel used in propelling a ship varies as the cube of her speed, and is $12.80 per hour when the speed is 8 miles per hour. The other expenses are $50.00 per hour. Find the most economical speed and the minimum cost of a voyage of 1000 miles.

42. An automobile manufacturer finds that 50,000 cars can be sold if each is priced at $4000. However, the number sold increases by 30 for every $1 decrease in the price. The manufacturer has fixed costs of $20,000,000; in addition, it costs $2000 to produce each car. How should the cars be priced to maximize profits?