Math 125 Hwk for Oct. 12 & 17

14a. Page 151 Derivatives of Implicit Functions

In Problems, 1 and 3, find dy\dx at the point indicated (a) by solving for y as a function(s) of x and finding the derivative of an explicit function and (b) by using implicit differentiation.

1. x²+2y = 1, (1,0)

3. y² = x+3, (1,2)

In Problems 5-13, find dy/dx.

5. x³ + y³ = 5

7. x^4/3 + y^4/3 = 1

9. x^1/3 + y^1/3 = 1

11. xy² = 4

13. 2xy-y² = 1

In Problems 15 and 17 find dy/dx at the point indicated (a) by solving for y as a function(s) of x and finding the derivative of an explicit function and (b) by using implicit differentiation.

15. x² + y² + 2y = 0, (0,2) 17. 3x² + 4xy + y² - 2y +7 = 0, (-1,3)

In Problems 19-31, find dy/dx.

19. (x+y)² = (x - y +1)²

21. x³ + 3x²y + y³ + 8 = 0

23. (x² - y² )² = 2x² + y²

25.

27. sinx = tany

29. tan(x+y) =y

31. x+y= cot (x-y)

33. At what point(s) does 3x²+y²+4x- 6y+1 = 0 have a horizontal tangent? A vertical tangent?

35. Find an equation of the line tangent to x² + y² - 6x - 8y = 0 at the point (6,0).

14b. Page 156 The Derivative 1-32 Odd

In Problems 1-5, find the indicated derivative.

1. y = 7x² + 2x -5, y'''

3. f(v) = (v² + 1)⁴ , f'''

5.

In Problems 7-11, find the indicated derivative and express the result in terms of x and y.

7. 2xy-y² = 5, d²y/dx².

9. x^2/3 + y^2/3 = 1, d²y/dx²

11.(x +y )² = 2xy + 5, d²y/dx²

In Problems 13 and 15, find f(x),f'(x),and f"(x) for the indicated value of x.

13. f(x) = 4x² -2x +1, x = 1

15.

In Problems 17 and 19, find dy/dx and d²y/dx² at the indicated point.

17. x² + y² = 25, (3,-4)

19.Ãx + Ãy = 1, (1/4, 1/4)

In Problems 21-27, position functions are given x in meters, t>0 in seconds, and the positive direction to the right. Analyze the motion as in Example 3, Page 155, and give a schematic diagram.

21. x = t³ - 2t² - 4t - 8

23. x = (t-3)³

25. x = 2t³ - 15 t² + 24 t

27.

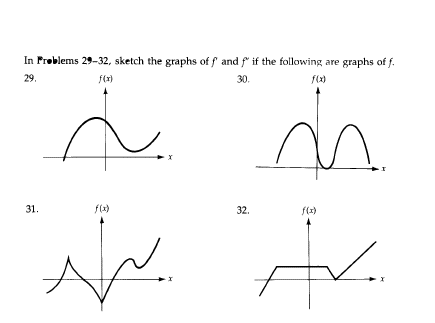
In Problems 29 and 31, sketch the graphs of f'and f" if the following are graphs of f.