Physics 213 Final 16 Points Each December 12, 2001

Instructor: K. W. Nicholson

1.

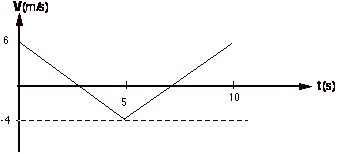
An object moves in such a way as to produce the velocity vs. time graph at the top of the page. Assume object starts at the origin.

a. Describe motion in words (Assume object begins at origin at t = 0.)

b. Draw the acceleration versus time graph.

c. Draw the displacement versus time graph. (Assume objects begin at origin at t = 0.)

d. Find the total distance travelled by the object.
2. George and Harry, riding in a truck traveling at a constant speed of 90 km/hr passes the more slowly moving Martha, who’s riding in her car. The instant the truck passes the car, the car begins to accelerate at a constant rate of 2 m/s/s and passes the truck 0.2 km farther down the road. What is the speed of the car when it passes the truck?

3. Gi-Gi, the famous Daredevil Gazelle has decided to try for a new gazelle distance record by being shot from a cannon. Her initial velocity will be 150 m/s ! The cannon is fired from a platform that is 100 m off the ground. The cannon is supposed to be aimed at an angle of 37E above the horizontal. But the guy hired to man the cannon doesn't really know how to operate it very well, and has no common sense. He sets the dial on the declination axis to -37Ethinking the minus sign is just a dash, and doesn't even notice that the cannon is pointed down 37E below the horizontal instead of instead of up 37Eabove the horizontal. So, how far from the base of the tower does Gi-Gi land?

4. a. Determine the mass M so that the 10 kg block will slide down the plane with constant velocity.

b. Explain,very carefully, in complete sentences, why the same mass will not work if the block is to slide up the plane.

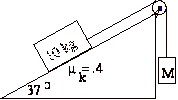
5. A 50 kg cart rolls down an incline as indicated in the picture. It starts from rest at a position that is a vertical distance of 45 m above the bottom of the incline. If it's speed when it gets to the bottom of the incline is only 20 m/s, what is the constant friction force caused by bad bearings in the wheels?

6. A 400 N kid rides a Ferris Wheel at the circus. She is sitting on a scales, to see how her weight (according to the scales ) varies as she goes around. The Ferris Wheel has a radius of 40 m and she is moving with a constant speed . If the strap holding her in the seat must exert a force of 100 N down to hold her in the seat at the top of the ride, how fast is she moving?

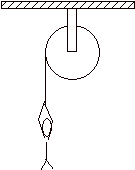
7. The solid disk has a mass of 100 kg and a radius of 3 m. The kid has a mass of 50 kg. The kid hangs from a rope that is wrapped around the disk. The kid starts from rest and falls a distance of 12 m before reaching the ground. How fast will the kid be travelling when she reaches the ground?

8. Find the moment of inertia of the system of particles below about the axis coming out of the page at location A.

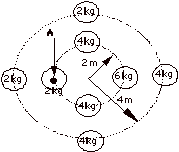
9. A 50 kg kid on a 200 kg bumper car is moving to the east at 30 m/s. He has a head-on perfectly elastic collision with another identical car that is moving west at 30 m/s and containing two large adults. The kid’s car bounces back in the direction from which he came at a speed of 100 m/s, while the adults car bounces backward at a speed of 5 m/s, how much do the two large adults weigh in newtons?

10. Fido the fat (205 kg) and his mistress Big Bertha (200 kg) are sitting on a stationary merry-go-round. Fido begins galloping clockwise around the merry-go-round a distance of 2 m from the center at a speed of 4 m/s. At the same BB begins to walk around the merry-go-round a distance of 4 m from the center in the opposite direction at 2 m/s. The merry-go-round rotates 0.5 rad/s.

a. what must be it’s moment of inertia?

b. Which way must it rotate, clockwise or counter clockwise?

11. A girl pushes with a force of 800 N on a 100 kg refrigerator (that glides on friction free rollers) for a time of 30 seconds . If the refrigerator is originally at rest, how much work has she done on the refrigerator?

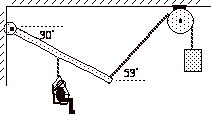
12. You are asked to design an Alternative Adult Relaxation Device (AARD). A person sits in a chair that hangs from the middle of a 2.0-m long, 10-kg uniform beam, as shown below. The seat bounces soothingly up and down with a little effort. Determine the mass of the object hanging from the rope that will keep the beam oriented as shown when a 60-kg person (including the mass of

the chair) hangs from the rope attached to the beam. Assume that g = 10 m/s² .