Physics 213 Test 3 Nov 8, 2002

Part I. Essentials, 5 points each

Note: In these problems you will write the appropriate equation, solve for the desired quantity, and substitute in the appropriate numbers, do NOT solve for the final number, nobody cares.

1. Moment of Inertia: (rotational mass) Determine the rotational mass of the system of masses in the figure if the system is pivoted about an axis perpendicular to the plane containing the masses and thru the center mass.

2. Conservation of momentum

a 60 kg kid on a 200 kg bumper car is moving to the east at 30 m/s. He has a head-on perfectly elastic collision with another identical car that is moving west at 30 m/s and containing two large adults. The kid’s car bounces back in the direction from which he came at a speed of 100 m/s, while the adults car bounces backward at a speed of 5 m/s, how much do the two large adults weigh in newtons?

3. A hoop of mass 50 kg and radius 3 m rolls along the ground at 5 m/s. What is it’s total kinetic energy?

4. t =Ia=rF sinu

A pulley of radius 3 m and a rotational mass of 50 kg m² has a weight attached by a rope . What will be the mass of the falling weight if it’s acceleration is 2 m/s²?

5. Impulse-momemtum:

If a 5 kg object has a change in momentum of 60 kg m/s in a time interval of 12 seconds, what applied force is required to accomplish this?

6. Conservation of angular momentum:

Fido the fat (200 kg) is sitting on a stationary merry-go-round. When Fido begins galloping clockwise around the merry-go-round a distance of 2 m from the center at a speed of 4 m/s, the merry-go-round rotates in the opposite direction 2 rad/s, what must be it’s moment of inertia?

7. t = r F sin u. A 3 m rod pivots about one end. A force of 20 newtons is applied to the other end at an angle of 30° with the direction of the rod. What is the torque produced by this force?

8. What are the 3 requirements for static equilibrium?

Part II. The Nitty Gritty: 10 points each

1. Really nasty can't believe he'd do this to us Rot Kinetic Energy problem.

We have here a massless hoop system, with 16 masses m attached as shown. It begins from the top of the incline that is 5 m high with initial speed v₀ = 20 m/s, how fast is it going when it reaches the bottom?

2. Definitions: Aft thrust engines propel a craft forward, forward thrust engines propel a craft backwards .

A 10⁶ kg space ship is moving forward at 600 m/s. A forward thrust engine that produces a force of magnitude 5 x 10⁶ N is employed for 30 seconds used to slow down the space ship.

a. What is the final velocity of the space ship?

b. How much energy was used in this manuver ?

c. What is the power output of the engine (assuming 100 % efficient)?

3. A woman whose mass is 90 kg stands at the rim of a horizontal turntable having a moment of inertia of 500 kg m² and a radius of 2m. Beside her is her faithful but very obese dog Fido, who's mass is 180 kg. The system is initially at rest, and the turntable is free to rotate about a frictionless, vertical axle through its center. The woman releases her pet Fido who begins to gallop in the counterclockwise direction at a speed of 4 m/s at a distance of 1 m from the rim. The lady then sits down on the outer edge of the turntable. In what direction and with what angular speed does the turntable rotate?

a. What principle is involved in solving the problem?

b. Draw a picture of the situation

c. Solve the problem

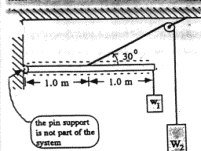
4. The beam has a mass of 8 kg, W₁ is 100 N. Mind the weight W₂ so that the beam is in equilibrium.

Note: a FBD for the beam is required, omitting one force costs 6 points, omitting a second costs an additional 3 points, a third, an additional 3 points etc. It is possible to get more points taken off than this problem is worth, so watch it!!