Physics 213 Test 3 Nov 17, 1999

Part I. Essentials, 5 points each

Note: In these problems you will write the appropriate equation, solve for the desired quantity, and substitute in the appropriate numbers, do NOT solve for final number, nobody cares.

1. Conservation of momentum

A 60 kg kid on a 20 kg skateboard is moving to the east at 30 m/s. He is holding his 30 kg cat . If he hurls the cat eastward at a speed of 20 m/s relative to the skateboard, what will be the kid on the skateboard's final velocity?

2. t= Ia=rF sinu

If a pulley of radius 3 m and a rotational mass of 50 kg m² has a weight of 60 N attached by a rope, what will be it’s angular acceleration?

3. Pendulum

If a grandfather clock were running fast, would you lengthen or shorten the pendulum to correct the time?

4. SHM

A Hooke’s law spring with spring constant 360 N/m suspended from a hook has a mass of 50 kg attached and set in to oscillation up and down. What is it’s angular velocity?

5. Law of gravity.

What is the acceleration due to gravity at an altitude equal to two radii of the earth above the earth?

6. Orbits

What must be the velocity of a satellite orbiting the earth a distance of 10⁹ m from the center of the earth?

7. Pressure

What is the total pressure at a depth of 8 m below the surface of a lake? (The density of water is 10³ kg/ m³ . Atmospheric pressure is 1.013x10⁵ N/m².)

8. Archimedes Principle

a. If a plastic ball has a density 3/4 that of water, what fractional part of it will be above the surface when it is floated in water?

b. If it floats in an unknown liquid with 1/2 of it above the surface, what must be the density of this unknown liquid? (The density of water is mentioned above).

Part II. The Nitty Gritty: 15 points each

1. Rot Kinetic Energy

If a solid disk begins rolling down an incline that is 3 m high with initial speed v₀ = 20 m/s, how fast is it going when it reaches the bottom?

2. Definitions: Aft thrust engines propel a craft forward, forward thrust engines propel a craft backwards .

A 10⁴ kg space ship is moving forward at 600 m/s. A forward thrust engine that produces a force of magnitude 5 x 10⁵ N is employed for 30 seconds used to slow down the space ship.

a. What is the final velocity of the space ship?

b. How much energy was used in this manuver ?

c. What is the power output of the engine (assuming 100 % efficient)?

3. A woman whose mass is 90 kg stands at the rim of a horizontal turntable having a moment of inertia of 500 kg m² and a radius of 2m. Beside her is her faithful but very obese dog Fido, who's mass is 180 kg. The system is initially at rest, and the turntable is free to rotate about a frictionless, vertical axle through its center. The woman then starts walking around the rim in a clockwise direction (looking downward) at a constant speed of 2 m/s relative to the earth. Fido is feeling playful and begins to gallop in the opposite direction at a speed of 4 m/s , only at a distance of 1 m from the rim. In what direction and with what angular speed does the turntable rotate?

a. What principle is involved in solving the problem?

b. Draw a picture of the situation

c. Solve the problem

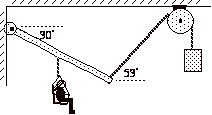
4. You are asked to design an alternative adult relaxation device. A person sits in a chair that hangs from the middle of a 2.0-m long, 10-kg uniform beam, as shown below. The seat bounces soothingly up and down with a little effort. Determine the mass of the object hanging from the rope that will keep the beam oriented as shown when a 60-kg person (including the mass of

the chair) hangs from the rope attached to the beam. Assume that g = 10 m/s .

Note: a FBD for the beam is required, omitting one force costs 6 points, omitting a second costs an additional 3 points, a third, an additional 3 points!