Appendix
4: Measuring Instruments
The
Metric Ruler: The scale of this metric measuring instrument is divided into
centimeters and millimeters. Since the millimeter is the smallest division on
the scale, the accuracy with which an object can be measured with this
instrument is limited to one millimeter. A reading to tenths of a millimeter
can only be estimated.
The
English Ruler: The smallest division on the scale of an English ruler is
one-sixteenth of a inch. Therefore, length an accuracy of one-sixteenth of an
inch.
The
Vernier Caliper:
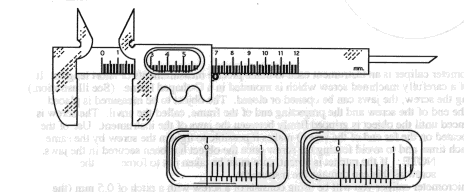
The
Vernier caliper is a metric measuring device which consists of a fixed part (a
fixed jaw and the main scale) and a movable jaw, which has a vernier scale
engraved on it. The vernier slides along the main scale so that the graduations
of the two scales can be compared. The fixed scale is divided into centimeters
and millimeters. The vernier scale is divided so that ten divisions on it
correspond to nine divisions on the main scale. Therefore, the length of each
vernier division is nine-tenths the length of a main-scale division. (See
illustrations.) When the jaws are closed, the zero line on the vernier (the
first line on the left end) coincides with the zero line on the main scale. In
this position, it can be seen that the first vernier division is 0.1 mm away
from the first main scale division, the second vernier division is 0.2mm away
from the second main-scale division, and so forth. If the jaws are opened
slightly, one can tell what fraction of a main-scale division the vernier index
(zero line) has moved by noting which vernier division coincides with a
main-scale division.
In
making a measurement with the vernier caliper, the jaws are dosed on the object
to be measured, and the position where the zero line of the vernier falls on
the main scale is noted. This reading gives a measurement that is accurate to
one millimeter. To obtain the fractional part of the main-scale division, the
line on the vernier which coincides exactly with a line on the main scale is
read. (See illustrations.) Therefore, the auxiliary scale of the vernier
enables one to make a measurement which is accurate to one tenth of a
millimeter.
If
the vernier does not read zero when the jaws are completely closed, a zero
correction -- either positive or negative -- must be applied to every reading.
The zero correction is always made be subtracting the zero reading from the
final reading.

The
micrometer caliper is an instrument used to make precise measurements of short
lengths. It consists of a carefully machined screw which is mounted in a
C-shaped frame. (See illustration.) By rotating the screw, the jaws can be
opened or closed. The object to be measured is placed between the end of the
screw and the projecting end of the frame, called the anvil. The screw is then
advanced until the object is gripped firmly between the jaws of the instrument.
Use of the ratchet (located on the far end of the screw) makes it possible to
tighten the screw by the same amount each time, and to avoid forcing the screw
once the object has been secured in the jaws. NOTE: If the ratchet is absent,
care must be taken not to force the screw as this can damage the instrument.
The
micrometer caliper you will be using consists of a screw with a pitch of 0.5 mm
(the distance advanced by the screw in turning through one revolution), a
longitudinal scale engraved along a barrel containing the screw, and a circular
scale engraved around a thimble which rotates with the screw and moves along
the scale on the barrel. The longitudinal scale is divided into millimeters,
while the circular scale has 50 divisions. Since the pitch of the screw is 0.5
mm, if the thimble is rotated through one scale division, the screw moves a
distance of one-fiftieth of 0.5 mm, or 0.01 mm. Therefore, measurements can be
made with an accuracy of 1/100 of a millimeter. Readings can be estimated to
1/1000 of a millimeter by estimating tenths of a thimble-scale
division.
The
micrometer is read by noting the position of the edge of the thimble on the
longitudinal scale (giving measurement to the nearest whole main-scale
division) and the position of the axial line of the barrel on the circular
scale (giving the fractional part of the measurement). The two readings are
then added together. since two revolutions of the screw are required for an
advancement of one millimeter, it is necessary to be careful to note whether
the reading on the circular scale refers to the first half or the second half
of the millimeter. (In the illustration, the reading is 7.75 mm.)
If
the micrometer does not read zero when the jaws are completely closed, a zero
correction -either positive or negative -- must be applied to every reading.
The value of the zero reading is made by noting the reading on the circular
scale when the screw is in contact with the anvil.
Formulas
DENSITY:
The density of a substance is defined as its mass per unit volume. Density can
be calculated mathematically using the formula:
where
m is the mass (which will be in grams for the Measurement Lab), V is the volume
(in cubic centimeters), and D is the density (in units of grams per cubic
centimeter).
![]()
VOLUME:
Volume can be defined as the measure of the capacity or space occupied by a
three dimensional figure (i.e.: a solid). Therefore, measurements of volume are
made in cubic units. The correct formula for finding the volume of an object
depends on the shape of the object. The volume of a cylindrical object is given
by the formula: where r is the radius, d is the diameter (2 r), and L is the
length (height) of the object being measured.
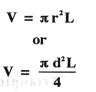
The
volume of a spherical object is given by the formula: ![]()
The
volume of an irregularly shaped solid can be determined by measuring the volume
of liquid that it displaces.
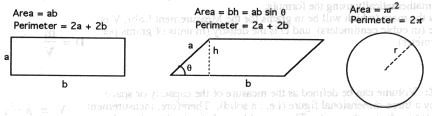
AREA:
Area is a measure of the size of a closed region, and is expressed as the
number of square units contained in the region. To find the area of a square or
rectangular shaped region, one simply multiplies its length times its width,
or: A = LW
To
find the surface area of an object with a curved surface (i.e.: a right
circular cylinder), one would use the formula: A = 2x rL
The
volume of an irregularly shaped solid can be determined by measuring the volume
of liquid that it displaces.
AREA:
Area is a measure of the size of a closed region, and is expressed as the
number of square units contained in the region. To find the area of a square or
rectangular shaped region, one simply multiplies its length times its width,
or: A = LW
To
find the surface area of an object with a curved surface (i.e.: a right
circular cylinder), one would use the formula: A = 2x rL
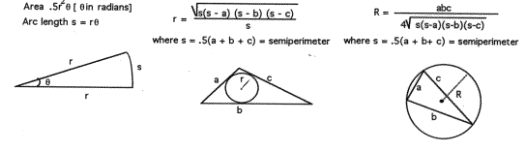
2-D
Geometric Shapes:
Rectangle:
Parallelogram
Circle
Triangle
Trapezoid
Polygon of n sides
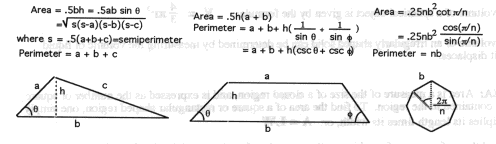
Radius of Circle circumscribing a
Sector of a
Circle
Radius of Circle inscribed
Triangle
in a Triangle
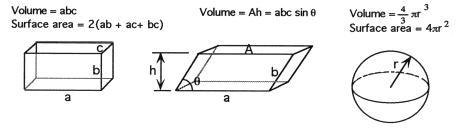
3-D
Geometric Shapes:
Rectangular
Parallel
piped
Parallelepiped
Sphere
Right
Circular Circular
Cylinder Pyramid
Cylinder
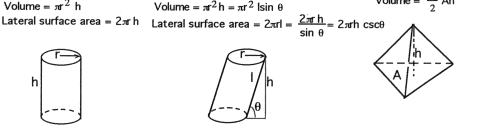
Spherical
Cap
Frustrum
Torus
