Appendix 6

The Method of Least Squares, Also Known As Linear Regression.

(Not for the weak of heart, but hang in there, it has a very happy ending.)

Quite often data consists of pairs of measurements (x_i and y_i) of an independent variable x_i and a dependent variable y_i. Suppose theory suggests that these data pairs can be fit by a straight line, so that you expect a straight line to result from a graph of y_i versus x_i. What you must then find are a pair of coefficients (A and B) such that y = Ax + B for any arbitrary x. An established method exists for determining the "best fit" to such data. This is the method of least squares.

A "best fit" is determined when the difference between the data (y_i) and the function Ax_i + B is minimized by an optimum choice of A (the slope) and B (the y intercept). This difference is denoted by y_i = y_i -(Ax_i + B). This minimization procedure is accomplished by minimizing a function called "chi-square" (x²). Where

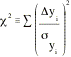
Where s_yi is the standard deviation of the sample of n measurements of y_i. If you rewrite the quantity y_i as y_i -(Ax_i + B), then x² becomes

x² =∑[(y_i - Ax_i - B)/s_yi]²

The function x2 is universally considered to be the appropriate measure of the "goodness of fit". Therefore when x² is minimized, a best fit is obtained.

As always, to minimize a function, one must set the derivative of that function equal to zero. The derivatives of 02 with respect to A and B are used since it is these coefficients which, in effect, must be varied to obtain the best fit. Taking these derivatives one obtains the following.

and

From these two equations, a pair of simultaneous equations results:

∑y_i = ∑Ax_i + ∑B and ∑ x_iy_i = ∑Bx_i + ∑Ax_i². The solution of this pair of equations is:

(6.3)

and (6.4)

where (6.5)

You may use equations (6.3) to (6.5) each time you wish to compute the slope and y-intercept from a set of x and y data pairs. Several simplifying assumptions have gone into these results, however this derivation will not be developed further. Suffice it to say that Eqns. (6.3) to (6.5) will do an adequate job of producing a best fit straight line throughout the labs in this course.

To obtain the error in the coefficients A and B it is necessary to follow the usual procedure of propagating uncertainties. This is quite laborious, therefore only the results will be quoted here.

If and retains its earlier definition,

then s_A² = (ns²)/ d and ∑B = (s²∑ x_i²)/ d.

Obviously, just using the formulas presented here for computing A, B, s_A², and s_B² can become quite a chore. Today, many scientific calculators contain built in algorithms for computing a best fit straight line. All of these algorithms utilize the method of least squares and the use of such a calculator is highly recommended. You should refer to the owner's manual of such calculators for explicit instructions on how to enter the pairs of x and y values into the calculator's memory. After the

data are entered, computing the coefficients A and B is as simple as computing the sine of an angle. I do not know whether or not any of these calculators automatically calculate s_A² and s_B², but some of them can be programmed to make these calculations. However, we have a nifty program in our computers called Graphical Analysis III that will calculate them for you !

*****************************************************