Wkb Chapter 7a

Lecture Notes on Momentum & Impulse

Definition: Momentum (designated P for some sicko reason) = mv

Definition: Impulse (denoted by I ! ) = chg in P = mv - mv_o = ∆ P

notice ∆P/∆T = m∆v/∆t = m ∆v/∆t = m a = F_avg

I = ∆P = F_avg ∆T but if F varies I = ∆P = ∫F dt or F_inst = dP/dt (original def. of F)

LAW OF CONSERVATION OF MOMENTUM - COMES FROM NEWTONS 3^RD

F₁₂ ∆t = -F ₂₁ ∆t

∆ P₁ = -∆P₂

m₁ v₁ - m₁ v_{10 =} - (m₂ v₂ - m₂ v₂₀) = m₁ v₁ + m₂ v₂ = m₁ v₁₀ + m₂ v₂₀

P = ∑P_i = P_o = ∑ P_io

Collisions 2 Kinds

Def. Perfectly in elastic collisions - hit and stick. P_f = P_o

(m₁ + m₂) v_f = m₁ v₁₀ + m₂ v₂₀ etc.

Def. Perfectly elastic collisions - hit and bounce off so that Kinetic Energy is conserved.

so

Discuss what happens when m₁ = m₂ ?

get out the moon & Earth, the horse and the roller thing.

Center of Mass - The point of balance - How to find it:

Center of mass of an object, or set of objects is the balance point for this object(s). To discuss this we really must introduce a related topic; Torque. Torque can be thought of as the tendency to make something rotate and officially, t r x F, where r is the distance from the pivot point (called the moment arm), and F is the force and x represents the cross product (Later).

Perspective:

Velocity v is the rate of change of distance w.r.t. time. Force F is a measure of an objects tendency to change velocity. Angular velocity about some axis of rotation is the rate of change of angle w.r.t. time.

Torque about some axis of rotation is a measure of an objects tendency to change angular velocity.

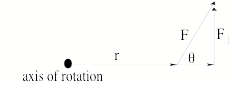
Definition: The magnitude of Torque t = r F , where r(called the moment arm), is the distance from the axis of rotation, to the point of application of force, and F is the component of force perpendicular to the moment arm. F = Fsin q, where q is the angle between the direction of r and the direction of F.

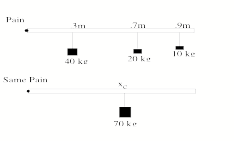
Now suppose we have a meter stick with masses attached like so. Pain is caused by torque t_@0

The center of mass of this system of objects is the balance point of the stick, but it is also the point at which all the mass could be located to get equivalent torque.

i.e. ∑m_igx_i = m_Tgx_cm , or x_cm = (∑m_ix_i)/m_T

Now suppose we had a set of point masses located in a two dimensional plane. The x_cm and y_cm could be found independently of one another in exactly the above fashion, so, y_cm = (∑m_iy_i)/m_T

Do example here with the set of mass points 2 kg at (-5,-2), 5 kg at (-2,2), 4 kg at (2,3), and 3 kg at (5,1).

Furthermore, if we wanted to obtain the center of mass of a two dimensional object, we could approximate its center of mass by dividing it up into rectangles, using the center of each rectangle as the center of mass of that rectangle, then obtain x_cm and y_cm as above. Then, in typical analytical fashion, we could take the limit as the number of rectangles goes to ∞, and bingo, we have another integral!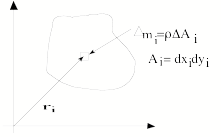

So, for planar objects, and

Now for a two dimensional object density r = mass/area = m/A= dm/dA

If we assume uniform density, then the density cancels out and we can just talk about the center of a plane region (called the Centroid of that region), in which case, the dm's above become dA's.

dA = dx dy, r_i = x_ii + y_ij so r_cm = (x_cm , y_cm), where

∫_Ax_c rdx dy ∫_A y_c dx dy

x_cm = ------------ and y_cm = ---------------- and x_c and y_c

∫_A rdx dy ∫_A dx dy

are expressions of the center of mass of the arbritrary mass point dm.