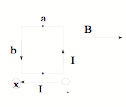
29.3 Torque on a Current Carrying Loop in Magnetic Field B:
t = BIAsin q, where q is the angle between B
and normal to loop.
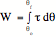
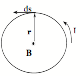
Ampere's Law: ŠBds = µoI, where I is the total current passing
thru the loop.
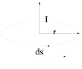 Blineds = Bline ds
cos 0, so ŠBds = BlineS =
Blineds = Bline ds
cos 0, so ŠBds = BlineS = 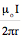 2¹r = µoI
2¹r = µoI
 -Uuseful to obtain B a
fixed distance from a current configuration
-Uuseful to obtain B a
fixed distance from a current configuration
- Like Gauss' Law for E,
most useful for symmetric configurations
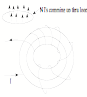
- Example: Find B a distance r from the center of
a toriodial coil with N loops.
Note: Total current passing thru the
constructed loop (dotted circle) of radius r is NI, B & ds are parallel, so ŠBds = NµoI, B is
constant, so ŠBds = B Šds = B2¹r =NµoI, thus, Btoroid = (NµoI) /
(2¹r)
Question: What would Bloop be if the
loop were drawn completely inside the toroid?
What would Bloop
be if the loop were drawn to completely enclose the entire toroid?
So, where would one use
a toroid?
30.4 Magnetic Field
inside a Solenoid
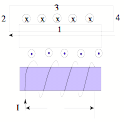
By Ampere's Law, Boutside
= 0, (net I thru any loop surrounding the entire solenoid = 0)
Bds = 0 on sides 2 &
4 because q = 90o, and
on side 3 because B = 0 outside the toroid
so, ŠBds = _1B ds + _2Bds + _3Bds
+ _4 Bds = BL + 0+0+0 = NµoI, so B = (NµoI)/L
= µonI
Note however that this
assumes that B is constant, so this formula only works in the middle of a long
solenoid. For short solenoids,
B(x) = (µoNI)/(2L)(sin q2 - sin q1)
Do #
Note that at the end of
a solenoid, q1 = 0 & q2 Å 900, so
Bend = 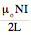 , and since at the
midpoint of the solenoid q1 = -q2 , Bmidpoint =
, and since at the
midpoint of the solenoid q1 = -q2 , Bmidpoint = 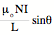
Magnetic Flux Fm = _BdA = BAcos q, (if B is
constant). It has units of Webbers
Wb = Tm2.
Gauss' Law for Magnetism: ŠBdA = 0, (compare to Gauss' Law for E, FE = ŠEdA = Qinside / eo)
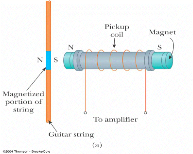
And where, you might
ask, would one use a solenoid? How
about electric guitars?

Ampere's Law
revisited. Why does a magnetic
field get produced between the plates of a capacitor when I changes direction,
(when it shoudn't, since no current flows between the plates, according to
Ampere's Law, B = µoI = 0)?
Well, because C = eoA/d, VC = q/c = Ed, so qplate = eoAE, so Ibtwn
plates = dqplate/dt = eoAdE/dt = eo dFE/dt !! This is called displacement current Id,
and the now complete Ampere's Law is
ŠBds = µo(I + Id),
and you won't be tested over it, but you heard it first here in Phy 214 at
CACC.
Summary
Biot-Savart Law - gives the magnetic
field at a point P due to a line of current I.
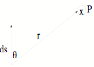 dB = [--- Unable To
Translate Text Box ---]
dB = [--- Unable To
Translate Text Box ---]
µo = 4¹x10-7 Tm/A
Ampere's Law: ŠBds = µoI, where I is the total
current passing thru the loop.
Magnetic Flux FB = _BdA , and
Gauss' Law for
Magnetism: ŠBdA= 0
Blong line
= µo I/(2¹a)
Bshort line = [--- Unable To Translate Text Box
---]
Bloop = 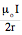
Btoroidial coil
= (µoNI)/(2¹r) where r is the mean radius of the toroid, and N is
the number of loops.
Bsole(x) = (µoNI)/(2L)(sin
q2 - sin q1)
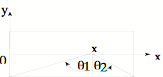
Bmidpoint = 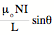
Bend of sole
= 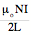
Bvery long = (µoNI)/(L)= µonI
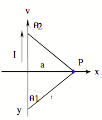
Motors and Generators
An AC generator is N
loops of wire rotating in a magnetic field with angular velocity w.
Then Fm = NBA cos (wt +qo) q = wt + qo, remember?
and xgenerated = - NAB (d/dt) cos(wt + qo) = NABwsin (wt + qo) What does xmax = ?
Current is thus produced and I = x /R
Now an AC motor is a
obtained by passing current thru N
loops of wire in a magnetic field.
The torque produced causes the motor to spin. Now since this torque is always perpendicular to the loop,
no work is done and once started, the unopposed motor should spin forever...
but it doesn't. Why not? Because of Lenz's Law. The rotating loop tries to set up a
current going in the opposite direction according to the formula for x for AC generators. So the useful work in an electric motor
is driven by the current I = xnet/R = (xapplied - xback)/R
Assign
Faraday's Law of Induction
Faraday's Law of
Induction - Electric fields are induced by a changing Magnetic flux.
- It says that a current
(and hence an emf) is setup in a closed conducting loop if the magnetic flux
thru that loop is changing with time, namely,
x = -dFm/dt =
-d(BAcos q)/dt, or, if have N
loops, x = -(N dFm/dt)
Note 1: x is induced if B, A, or q changes in time!
Note 2: The negative sign is a consequence of
Lenz's Law, which says the current induced will be in a direction so that the
magnetic field it creates will try to prevent a change in Fm.
do ,
Assign
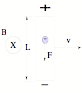 Example 1: Suppose you have a conductor moving in
a magnetic field. The charges in
the conductor feel FB = qvB, and the electrons will continue to move
until the potential difference between the ends of the conductor is strong
enough to produce an electric field that equalizes the magnetic force. i.e. FE = qE = qvB, or E = vB. Note: x = Blv
Example 1: Suppose you have a conductor moving in
a magnetic field. The charges in
the conductor feel FB = qvB, and the electrons will continue to move
until the potential difference between the ends of the conductor is strong
enough to produce an electric field that equalizes the magnetic force. i.e. FE = qE = qvB, or E = vB. Note: x = Blv
do
, Assign
Example 2: Find the power delivered by the applied
force Fapp in the diagram to the resistor R.
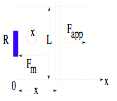 Fm = BA =
Blx, x = -dFm/dt = Blv =
IR, so I = Blv/R . Now the force
on the moving conductor (line of current), is Fm = BIL. Constant velocity means Fm =
Fapp, so the power delivered by Fapp to R is P = Fappv
= Fmv = (BIL)v = B (Blv/R) lv = B2L2v2/R
Fm = BA =
Blx, x = -dFm/dt = Blv =
IR, so I = Blv/R . Now the force
on the moving conductor (line of current), is Fm = BIL. Constant velocity means Fm =
Fapp, so the power delivered by Fapp to R is P = Fappv
= Fmv = (BIL)v = B (Blv/R) lv = B2L2v2/R
Do #, Assign #
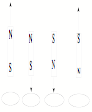 Lenz's Law: Remember, motion toward the loop implies
Bincreasing and motion away from the loop implies Bdecreacing
Lenz's Law: Remember, motion toward the loop implies
Bincreasing and motion away from the loop implies Bdecreacing
Examples: Do all possible combinations with the
loop and a magnetic.
Induced emfs and Electric fields
do . Note: x = n Eds = -dFm/dt =
d(BAcos q)/dt = (d/dt)(BA1cosq) + (d/dt)(BA2
cos q) = µoNA/L(dI/dt)
+ 0
Assign
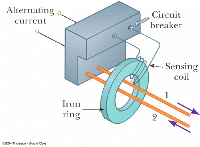
Inductance
What happens when the
switch is thrown? The current in
the wire creates a magnetic field Binc into the page inside the
loop. This ÆFm creates
xind that
tries to send current back the other way.
xind = -NÆFm/dt =
-NÆ(BAcos q)/dt. But in any fixed circuit, q = 0, A is fixed,
and B is
some constant multiple of I, hence, -NÆFm/dt = -LdI/dt, where L is this
constant, is called Inductance,
has units of Vs/A = kg m2/C2 = Henry's (H). Integrating both sides with respect to
t yields NFm = LI, or L = NFm/I (official definition of Inductance), so
xind = xL = xback =
-LdI/dt, or L = -xind /(dI/dt).
In particular, for a solenoid of length L, Lsole = N2µoA/ L = constant ! (like capacitance).
Do 2 & 10, Assign
3,7,9
 32.2 RL Circuits How does the current behave? By the loop rule, x - IR -LdI/dt = 0, a differential equation whose
solution produces:
32.2 RL Circuits How does the current behave? By the loop rule, x - IR -LdI/dt = 0, a differential equation whose
solution produces:
Charging: I = (x/R)(1 - e-Rt/L) = (x/R)(1 - e-t/t), where t = L/R called the RL
time constant.
Discharging: I = (x/R)e-t/t = Ioe-t/t. Note: t is the time it takes I to reach 1-e-1
= .63 of its maximum value.
Do
, Assign
32.3 Energy stored in an inductor. Um =  LI2, Um sole = B2
AL/(2µo)
LI2, Um sole = B2
AL/(2µo)
Do 14, 18,22 , Assign .
Mutual Inductance M2 due to 1 N2F2 due to 1/I1
, x2 = -N2
dF2 due to 1 /
dt = -M2 due to 1(dI/dt)
 Do 30,36 , Assign
Do 30,36 , Assign
32.5 LC Circuits U = Uc + UL = Q2/(2C) + LI2/2
When the switch is
thrown, with the capacitor charged up, we get the loop equation Ld2Q/dt2
+ Q/C = 0, which is the dif. eq. of motion for Simple Harmonic Motion (SHM),
with angular frequency w = 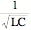 , moreover, at time t,
, moreover, at time t,
Q = Qmax cos
(wt + d), and I = -Qmaxwsin(wt + d), do46, 48, Assign
47,49,53
32.6 RLC Circuits Is like a damped harmonic oscillator
Q = Qme-Rt
/ (2L)cos(wdt), with wd = 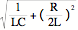 Rc=(4L/C).5
Rc=(4L/C).5
Do # 54, Assign # 55
AC Circuits
1 Pure Resistive Circuits
current does not affect vR , so iR and vR
are in phase
v = Vmax sin wt, w = 2¹f = 2¹/T
vR = Imax
R sin wt
iR = v/R = (Vmax/R)sin
wt = Imaxsin wt
P = i2R
Root mean square voltage
and current: a kind of average
value vrms
= v /Ã2, irms = i /Ã2
2 Pure Inductive Circuit: current lags
voltage 90o The voltage dropped across an inductor is the induced xback which is
created by changing magnetic flux, and is greatest when the switch is first
thrown, hence, current lags voltage 90o.
v + vL = 0 =
v - Ldi/dt, from whence, v = vmax sin wt, and iL = (Vmax/wL)sin (wt - ¹/2)
Imax = Vmax/(wL) = Vmax/cL , cL = wL = Inductive Reactance
and has units of ½ !
vL = Vmax
sin wt = Imax cL sin wt
3 Pure Capacitive Circuit: current leads voltage by
90o Potential difference across the capacitor is maximum after the
current dies, hence current leads voltage by 90o in a capacitive
circuit.
v - vC = o,
from whence v = vc sin wt = q/C, and q = CVmax sin wt, so i = dq/dt = wCVmax cos wt = wCVmax sin(wt - ¹/2)
Imax = wCVmax = Vmax
/cC . cC = 1/(wC) = 1/(2¹fC), is called capacitive reactance
and has units of ½. vc
= Imax cC sin wt
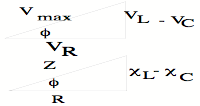
4 RLC series Circuits
v = Vmax sin wt = vR + vC
+ vL
i = Imax sin(wt - f) and is the same in all
elements in the circuit
f = 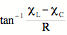
Vm = 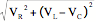 = Imax
= Imax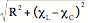 = Imax Z
= Imax Z
Resonant (angular)
frequency wo occurs
where cL - cC = 0, or
when wL = 1/(wC), so wo = 1/ÃLC
33.5 Power in AC Circuits
Pavg = .5 Imax Vmaxcos f (cos f is called the power factor)
= Irms
Vrms cos f
= Irms2R
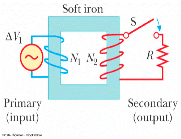
5 Transformers: N1V1 = N2V2,
and I1 V1 = I2 V2
Assign:
![]() µo
= 4¹x10-7 Tm/A
µo
= 4¹x10-7 Tm/A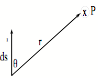
![]() direction
of B: New right hand rule!
direction
of B: New right hand rule!![]()
![]()
![]()
![]()
![]()
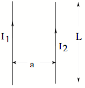 Example 3: Find Force on
one line of current due to one parallel to it.
Example 3: Find Force on
one line of current due to one parallel to it.![]()

















