Wkb Chapter 3, C&S Chapters 3 & 4 : Electric Fields

Discuss fields in general, E = electric field

H = gravitational field

B = magnetic field

Show the Mechanical Universe Film on Electric Fields

Read aloud paragraphs 1 - 3 in 3.1.1.

Discuss the picture.

Show the Phet Simulation for Electric Fields, also the active figures.

Then clear up the confusion about Electric Field vectors and Electric Field lines immediately by discussing Eric Mazur's 2 Quizzes.

Definition: The electric field due to charge Q is defined to be E_Q = F _{Q on q} / q

But notice the E doesn't depend on q at all. In fact, the electric field due to Q , a distance of r from Q, is given by

E_Q (r) = kQ/r²

It has units of N/C

Definition: The positive direction in an electric field is the direction a positive charge would move in the field.

Problem: If a +3 nC charge experiences a force of 5x10² N to the right, what is the magnitude and direction of the elecctric field at that location?

Drill (home made): Do 4 problems. Given the E-field at particular location, find the magnitude and direction of the force on a given charge q.

Problem: Given charge Q and distance r from Q, find the direction and magnitude of electric field produced.

3.1.6 Memorize the patterns of E field vectors near + and - charges. Note the different conventions for + and - charge E-Fields in C&S text, pg 91.

Do 3.1.6a now.

3.1.7 Note: points radially outward from Q, the charge causing the electric field.

3.2 Superposition principle. (1 & 2 dimensional E-Field problems) Find the force on q₁ due to all the other charges combined , then find the force on q₂ due to all the other charges combined, etc. for the following charge configuration.

3.2.1 Read aloud.

Assign 3.2.2a & b

3.3 Electric field due to a dipole: (See also ActivPhysics 11.3 Question 4 ) Some really kinky behavior of charged tapes explained. (optional)

Read it and try 3.3.3e

Read down to 3.3.4 and do 3.3.3f

3.3.4 E-field inside conductors

(RBD) is always zero under static equilibrium conditions.

is not zero under non-static equilibrium conditions.

Discuss the peanut on page 101.

Do 3.3.4a

Do 3.4a

3.4.1 Conditions under which E = F/q Read page 104 & 105, the paragraph below the second box on page 105 is the Heisenberg Uncertainty Principle.

3.5 E -Field, what is it really? What Michael Faraday first invented as a "prop" to explain his ideas has taken on a life of its own.

Do Hwk 3-6 and discuss field lines.

Assign RQ3: 1-5, 7, 9 &10, Homework 3: 1,2,4,5

Electric Fields

All masses create a gravitational field, which gives the strength of the gravitational attraction at a given distance from the center of the mass. For instance, the strength of the Earth's gravitational field at the surface of the Earth is g = (GM_E)/R_E² = 9.8 m/s² = F_g /m_o for ANY mass m_o a distance of R_E from the center of the earth. Notice this field value depends only upon the distance from the center of the earth's mass, so it could more accurately be written g(r) = GM_E/r² at any distance r from the center of the Earth. Or, turned around, the force on an object m at a location where the strength of the gravitational field is g, is F_g = mg.

Likewise, all charged objects create electrical fields E = F_E/q_o = kQ/r² at a distance r from the center of an object with charge Q. Or, turned around, the force on an object with charge q at a location where the field due to an object of charge Q was E would be F_E = qE. There is one difficulty however, while all masses are attracted toward the Earth's mass, charged objects could be either attracted to or repelled from the object with charge Q, depending upon whether the objects have unlike or like charge respectively. So some convention regarding the direction of an electric field must be defined: hence, the direction of the electric field is defined to be the direction a Positive charge would be driven by the object's charge Q.

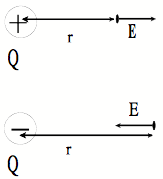
In summary then: E = kQ/r² , or E = F_E/q , and F_E = qE .

Steps to finding total E .

1. Draw frame of reference (coordinate axes).\

2. Draw a free body diagram for the point in space.

3. Find the magnitude of each E.

4. Find the x & y components of each (Pay attention to the signs of these).

5. Add the x components and then the y components to find the x and y components of the total E.

6. If necessary, use Pythagoras’ Thm to find the magnitude of the vector.

7. Use the inverse tangent function to find u = tan^{-1 (F}_y^/F_x^{) .}

III. Electric field lines, the density of these lines indicate the strength of an electric field at a particular location.

IV. Acceleration of charged particles in an electric field E.

Since F_E = qE = ma (remember old Mr Newton?), acceleration a = qE/m.

How does one determine the electric field at a particular location due to several charges ? Well, E's are vectors, so they're additive. E = ∑(kQ_i)/r_i², or if the set of charges is infinite, E = _kdq/r², (see examples 8,9 and 10 in chapter 23). Note: the electric field in the vicinity of various geometric configurations of uniformly charged bodies is located at the end of chapter 24.

At this point do heavy duty drill on 2 dimensional problems.
Chapter 4: Electric Fields due to continuous Charge distributions

At the very least, you need to set up the expression.

Both setting up and evaluating integrals is a bit of an art, but you really need to make an effort to master basics.

Numerical integration is often the way to go, either for simplicity, or because the expression is not integrable. Study C&S pgs 126 and 127.

Steps (C&S pg 122) altered slightly. (one added) 0. Choose coordinate system wisely.

Examples:

1. Find the electric field due to the ring at a point along the axis.

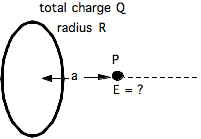
2. Same as above, only a solid disk.

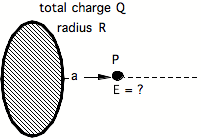
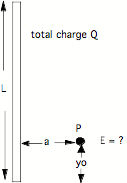
3. Electric field at the point indicated, due to a rod.

4.5 Two uniformly charged disks: a capacitor.

Notice that as s gets smaller and R get bigger relative to s, the fringe field outside the disks tends toward zero. The further apart the disks are, the stronger the fringe fields are.

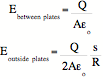
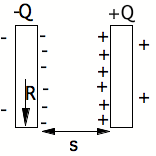
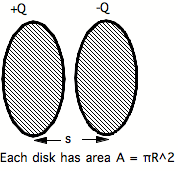
Be able to show these equations from the definition of E_{ring a distance x from center on axis} =

Be able to use the above formula to find E_disk(x) a distance x along the axis of a disk.

Do 4.5 a,b

Assign 4.5 c,d

Do 4.5 e

4.6 E-field due to a spherical shell: Acts like a point charge outside the sphere, (means you can assume all the charge on the sphere is located at its center), because of the 1/d² nature of E, and is zero everywhere inside the shell, conductor or non conductor, for the same reason. See 4.6a

E inside a conductor is always zero.

Assign, 4.6.3 b & c

Assign: RQ4-all, Hw4:4,5,7,9,10 - 13;
Lightning Explained

Q. Can lightning strike up from the ground to a cloud?

A. This is a commonly asked question, to which the answer is both yes and no. Lightning, in it's simplest definition, is a discharge of electricity, which occurs in mature thunderstorms. Although we might expect lighting to come down from the clouds like the rain does, lightning actually occurs dynamically between the

thunderstorm and the ground. Approximately one out of five lightning "strokes" actually hits the ground. These are referred to as cloud-to-ground strikes. The complete lightning strike process is a series of steps, all of which happens in a few millionths of a second and thus appears as one motion to the human eye.

The lightning process begins with the bottom side of the cumulonimbus cloud, or thunderstorm, becoming negatively charged with electricity. This charged cloud polarizes the ground below causing the ground beneath the thunderstorm to have an induced positive charged. This positive charge on the ground is most pronounced in objects extending above the ground, such as tall trees or buildings. The negative charge in the base of the thunderstorm continues to grow until a series of very faint and small strikes, called "stepped leaders", strikes in succession, each extending approximately 50 meters lower than the previous. As the stepped leaders near the ground, a current of positive charge starts up to meet it (again, this is usually from an object extending above ground). When the two meet, a flood of the negatively charged electrons flows into the ground, followed immediately by a positive charge rushing back up the path of the stepped leaders into the cloud. This is called the "return stroke" and is a much larger and brighter stroke than the proceeding stepped leaders, and this is what we

actually see. Again, all this happens virtually simultaneously and just appears as a quick bolt of lightning to us. Thus, lightning starts from the clouds, but it is the return stroke from the ground that we see.